Study on Beta Diversity of Ancient and Famous Trees in Taizhou
-
摘要:
本文基于2017年浙江省台州市的古树名木调查结果,将台州全市分别按经度0°10′、纬度0°10′或海拔100 m的梯度划分单位,研究该市古树名木β多样性的空间梯度格局。结果表明:(1)台州市的古树名木总体β多样性在沿纬度、经度或海拔梯度均主要由树种的空间轮转决定。(2)沿纬度、经度或海拔梯度,对基于多度的总体β多样性贡献最大的前8个树种均为云锦杜鹃Rhododendron fortunei、樟Cinnamomum camphora、马尾松Pinus massoniana、柳杉Cryptomeria japonica var. sinensis、甜槠Castanopsis eyrei、枫香树Liquidambar formosana、苦槠Castanopsis sclerophylla、柏木Cupressus funebris。(3)两相邻区位间的Sorensen指数值、Jaccard指数值、Bray-Curtis指数值和Morisita-Horn指数值随纬度的增加呈现出先增大后减小的趋势;无论是基于多度还是有无二元法,8号区位(位于29°10′0″~29°20′0″ N)对总体β多样性贡献最大。两相邻区位间的Sorensen指数值、Jaccard指数值、Bray-Curtis指数值和Morisita-Horn指数值随经度的增加呈现先小后大的波浪曲线变化趋势,无论是基于多度还是有无二元法,5号区位(位于120°0′0″~121°10′0″ E)对总体β多样性贡献最大。两相邻区位间的Sorensen指数值、Jaccard指数值、Bray-Curtis指数值和Morisita-Horn指数值随海拔的增加呈先大后小的波浪曲线变化的趋势,无论是基于多度还是有无二元法,1号区位(位于海拔1~100 m之间)对总体β多样性贡献最大。本研究结果表明,沿纬度、经度或海拔梯度,在全市分布较为普遍且集中的树种基于多度的总体β多样性贡献最大,株数只有几株或几十株但分布比较均匀的树种,基于有无二元法的总体β多样性贡献大;在选择β多样性指数时,不能仅考虑测度计算方法的简便易用,还需考虑每一物种的个体数量或相对多度等信息,以免稀疏种在区位中的作用被夸大,以致得出不合理的结论。
Abstract:Based on the 2017 survey results of ancient and famous trees in Taizhou City, Zhejiang Province, this study divides the city into units according to 0°10′ longitude intervals, 0°10′ latitude intervals, or 100 m elevation intervals, and investigates the spatial gradient patterns of beta diversity among ancient and famous trees in the city. The results showed that: (1) The overall β diversity of ancient and famous trees in Taizhou City is mainly determined by the spatial rotation of tree species along latitude, longitude, or altitude gradients. (2) The top eight species contributing most to overall beta diversity based on abundance were consistent across latitude, longitude, and elevation gradients: Rhododendron fortunei, Cinnamomum camphora, Pinus massoniana, Cryptomeria japonica, Castanopsis eyrei, Liquidambar formosana, Castanopsis sclerophylla, and Cupressus funebris. (3) The Sorensen, Jaccard, Bray-Curtis, and Morisita-Horn indices between adjacent regions initially increased and then decreased with increasing latitude. Regardless of abundance or presence-absence binary methods, Region 8 (29°10′0″-29°20′0″ N) contributed most to overall beta diversity. Along the longitudinal gradient, these indices exhibited a wave-like pattern of initial decrease followed by increase. Region 5 (120°0′0″−121°10′0″ E) showed the highest contribution to beta diversity. Along the elevational gradient, the indices displayed a wave-like trend of initial increase followed by decrease, with Region 1 (1−100 m elevation) contributing most significantly. The findings indicate that species with wide and concentrated distributions contribute most to beta diversity when abundance-based metrics are used, while species with sparse but uniform distributions contribute more under presence-absence binary methods. When selecting beta diversity indices, it is essential to consider species abundance or relative dominance to avoid overestimating the role of rare species, which may lead to biased conclusions.
-
生态学家Whittaker最早于1960年提出Beta多样性(β多样性)时将其定义为“与环境的复杂梯度或环境格局相联系的群落组成变化的幅度或群落分化的程度”,并于1972年发表论文专门阐述了Beta多样性的概念及其度量方法。经过数十年的讨论与完善,现在学界一般认为Beta多样性是指不同群落间物种组成的变化,由物种周转(或物种替换)和嵌套(或丰富度差异)这两种过程决定。由于Beta多样性丰富的内涵,对其理论及测度方法的研究一直受到生态学家们的关注,围绕其展开的学术讨论也一直持续到现在。
Whittaker认为可以用物种有-无数据或物种多度数据来测度群落的Beta多样性,目前的相关研究也多基于此进行,当群落的物种替代率或周转率是沿一定生态梯度(空间、时间或环境)分布时常采用前者,而在生态排序中,若研究沿某一特定梯度具有单峰分布特征的物种的周转率则常用物种多度数据进行。生态学家们提出了许多种度量Beta多样性的方法,分别从不同的角度对物种组成在时空尺度上的变化进行评价。在倍数关系分配方法(Beta与Alpha的乘积为Gamma)和总和关系分配方法(Beta与Alpha的和为Gamma)中,Beta多样性是与Alpha多样性和Gamma多样性在数值上相关的导出量。当独立计算群落Beta多样性指数时,学者们提出以相似性(相异性)指数来进行度量,主要有基于物种有-无数据的Sørensen指数、Jaccard指数和Simpson成对相异性指数等,还有基于物种多度数据的Bray-Curtis指数。Legendre等提出,可以通过计算样方-物种多度矩阵的总方差来估算Beta多样性,进而探究总方差可解释部分中环境因子和空间因子作用强度, 这样有助于分析环境过滤主导的生态位过程和扩散限制主导的中性过程的相对重要性。在探讨物种周转和嵌套这两种过程对群落物种组成差异的影响时,需要对Beta多样性进行分解以对这两个过程进行量化。目前主流的分解方法为BAS法和POD法,前者基于Sørensen指数提出,将总体Beta多样性分解为空间周转组分和嵌套组分;后者基于Jaccard指数提出,将总体Beta多样性分解为物种空间替换组分和物种丰富度差异组分。由于Beta多样性具有空间尺度依赖性,除了最终的分析尺度,研究范围和取样间隔等主观条件也会影响结果,但群落所处的纬度梯度、地形地貌和时间推移所造成的各项条件变化(如气候变化)等客观条件才是影响Beta多样性的本质因素。
全国绿化委员会在《关于进一步加强古树名木保护管理的意见》(全绿字〔2016〕1号)中对古树名木作出如下定义:古树是指树龄100年以上的树木,名木是指具有重要历史、文化、景观与科学价值和具有重要纪念意义的树木。古树名木是其生长所在地悠久的历史与文化象征,记录着当地的自然变迁、人类活动、森林演替、气候和地质等环境的变化历史[1],具有极高的科研价值、美学价值、经济价值、文化价值和欣赏价值。随着乡村振兴战略和生态文明建设的推进,对古树名木资源的保护、研究和开发利用也越来越受到重视。研究者针对古树名木的分布格局、多样性、保护和价值计量等方面已进行了大量的研究[1–10],也有学者研究了地带性森林群落物种多样性[11],但对于古树名木β多样性的空间梯度格局尚少见报道。笔者根据2017年浙江省台州市古树名木普查数据,利用生物多样性指数,研究台州市古树名木β多样性的空间梯度格局,旨在为台州市古树名木的保护提供参考依据。
1. 材料和方法
1.1 研究区概况及调查方法
1.1.1 自然概况
台州市位于浙江省中部沿海,地理坐标为28°01′~29°21′ N,120°17′~121°56′ E,陆地总面积为9 411 km2,下辖3区、3市和3县,地势西高东低,地貌类型多样,其中山地丘陵约占70%,土壤以红壤、黄壤、水稻土和粗骨土为主,滨海平原有少量盐土和潮土,有“七山一水二分田”之称。属中亚热带季风气候区,四季分明,冬无严寒,夏少酷热,热量丰富,雨水充沛。年均气温为16.6~17.5 ℃,年均降水量约为1 630 mm,相对湿度在78%~83%,无霜期为235~322 d。灾害性天气主要有台风、暴雨、旱涝、寒潮等。台州市域内既有山区、平原,又有海岛、滩涂,生境多样,植被类型众多。地带性植被属中亚热带常绿阔叶林,植被类型主要有温性针叶林、暖性针叶林、常绿阔叶林、落叶阔叶林、针阔混交林、常绿落叶阔叶混交林、竹林、山顶苔藓矮曲林、灌草丛和人工植被等[10,12–13]。
1.1.2 调查方法
2017年,台州市各县(市、区)根据浙江省林业厅统一部署,分别开展所辖行政区域内的古树名木普查工作。主要采取访谈法(走访本地相关人员)、文献分析法(调阅历史普查数据)、现场实地调查法等开展普查。普查的内容包括:古树名木的树种名称、地理位置、健康状况、权属、年龄、坡度、海拔、胸径、树高、冠幅、坡向、坡位等。古树名木所处的海拔、经纬度用手持PDA测定,树高用测高仪测定,胸径用围尺测定,冠幅用皮尺测定;以查阅历史资料、询问当地相关人员等方式记录树龄,同时记载保护状况。
1.2 β多样性指数及分解
本研究采用Sorensen指数($ {C}_{s} $)和Jaccard指数($ {C}_{j} $)等有无二元属性测度方法(也叫相似性系数测度方法),以及Bray-Curtis指数($ {C}_{N} $)和Morisita-Horn指数($ {C}_{MH} $)等数量测度方法来计算β多样性指数[14-16],其计算公式如下:
$$ {C}_{s}=\frac{2c}{a+b} $$ (1) $$ {C}_{j}=\frac{c}{a+b-c} $$ (2) $$ {C}_{N}=\frac{2jN}{a+b} $$ (3) $$ {C}_{MH}=\frac{2\sum ({an}_{i}\times {bn}_{i})}{(da+db)\times a\times b} $$ (4) 式(1)~(4)中,c为两个区位共有的树种数,a、b分别为区位1和区位2的树种数,jN为区位A(jNa)与区位B(jNb)共有树种中多度较少者之和,即$ jN=\sum \mathrm{m}\mathrm{i}\mathrm{n}(jNa,jNb) $,ani和bni为区位A和区位B中第i个树种的多度,$ da=\sum {an}_{i}^{2}/{a}^{2} $,$ db=\sum {bn}_{i}^{2}/{b}^{2} $。
基于有无二元法的β多样性指数(βsor)可以分解为树种轮转组分(βsim)和树种嵌套组分(βsne)[17],其计算公式如下:
$$ {\beta }_{\mathrm{s}\mathrm{o}\mathrm{r}}=\frac{a+b}{2c+a+b}\equiv {\mathrm{\beta }}_{\mathrm{s}\mathrm{i}\mathrm{m}}+{\mathrm{\beta }}_{\mathrm{s}\mathrm{n}\mathrm{e}} $$ (5) $$ {\beta }_{\mathrm{s}\mathrm{i}\mathrm{m}}=\frac{\mathrm{m}\mathrm{i}\mathrm{n}(a,b)}{c+\mathrm{m}\mathrm{i}\mathrm{n}(a,b)} $$ (6) $$ {\beta }_{\mathrm{s}\mathrm{n}\mathrm{e}}=\frac{\left|a-b\right|}{2c+a+b}\times \frac{c}{c+\mathrm{m}\mathrm{i}\mathrm{n}(a,b)} $$ (7) 式(5)~(7)中,c为两个区位共有的树种数,a、b分别为区位1和区位2独有的树种数。
基于多度的β多样性指数(Btotal)则可以分解为树种周转组分(Repl)和树种多度差异组分(AbDiff)[18-19],其计算公式如下:
$$ {B}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\frac{A+B}{2C+A+B}\equiv {R}_{\mathrm{e}\mathrm{p}\mathrm{l}}+{Ab}_{\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}} $$ (8) $$ {R}_{\mathrm{e}\mathrm{p}\mathrm{l}}=\frac{2\mathrm{m}\mathrm{i}\mathrm{n}(A,B)}{2C+A+B} $$ (9) $$ {Ab}_{\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}=\frac{\left|A-B\right|}{2C+A+B} $$ (10) 式(8)~(10)中,C表示两个配对区位中每个树种在两个区位中的最小多度的总和;A表示两个配对区位中区位1的总多度减去C的差值;B表示区位2的总多度与C的差值。
1.3 区位与树种对β多样性的贡献度
Legendre等提出用区位的树种组成矩阵的总方差作为β多样性的度量[20-25]。总体β多样性($ {BD}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}} $)、单个树种对总体β多样性的贡献($ {SCBD}_{j} $)、单个区位对总体β多样性的贡献($ {LCCBD}_{i} $),其计算公式如下:
$$ {BD}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\mathrm{v}\mathrm{a}\mathrm{r}(Y)=\frac{\sum\limits _{i=1}^{n}\sum\limits _{j=1}^{p}({y}_{ij}-{\overline{y}}_{j})^{2}}{n-1} $$ (11) $$ SCBD_j=\frac{\sum\limits_{{{{{{{i}}}}}}=1}^{{{n}}}({{{y}_{{i}{j}}}}-{{{\overline{{y}}_{{j}}}}})^2}{\sum\limits_{{{{{{{i}}}}}}=1}^{{{n}}}\sum\limits_{{{\mathit{j}}}=1}^{{{p}}}({{{y}_{{i}{j}}}}-{{\overline{{y}}_{{j}}}})^2} $$ (12) $$ {LCCBD}_{i}=\frac{\sum\limits _{{j}=1}^{{p}}({{y}}_{{i}{j}}-{\overline{{y}}}_{{j}})^{2}}{\sum\limits _{{i}=1}^{{n}}\sum\limits _{{j}=1}^{{p}}({{y}}_{{i}{j}}-{\overline{{y}}}_{{j}})^{2}} $$ (13) 式(11)~(13)中:BDtotal、var(Y)为各区位树种组成矩阵Y的总方差,n表示区位数,p表示树种数,yij表示第j个树种在第i个区位内的有无或多度,$ {\overline{y}}_{j} $为树种j在全部区位中的平均值。
2. 结果与分析
根据调查,台州全市古树名木共计15 668株,其中古树15 654株、名木14株,隶属于56科、117属、194种。从树种组成看,古树名木各树种中株数在1 000株以上的有樟Camphora officinarum 3 026株,占总株数的19.31%;云锦杜鹃Rhododendron fortunei 2 214株,占总株数的14.13%;马尾松Pinus massoniana 1 928株,占总株数的12.31%;枫香树Liquidambar formosana 1 463株,占总株数的9.34%;苦槠Castanopsis sclerophylla 1 325株,占总株数的8.46%;柳杉Cryptomeria japonica var. sinensis 1 013株,占总株数的6.47%。从树龄结构看,树龄299 a以下的古树名木有13 675株,占总株数的87.28%;树龄300~499 a的古树名木有1 431株,占总株数的9.13%;树龄500 a以上的古树名木有562株(其中树龄1 000 a 以上的古树名木有57株,最大树龄为1 600 a), 占总株数的3.59%。就生长势而言,生长势正常的古树名木有14 502株,占总株数的92.56%;生长势衰弱的古树名木有883株,占总株数的5.63%;生长势濒危的古树名木有283株,占总株数的1.81%。按县(市、区)行政区域分,椒江区有77株,占总株数的0.49%;黄岩区有982株,占总株数的6.27%;路桥区有41株,占总株数的0.26%;临海市有1 532株,占总株数的9.78%;温岭市有254株, 占总株数的1.62%;玉环市有178株,占总株数的1.14%;天台县有7 134株,占总株数的45.53%;仙居县有4 786株,占总株数的30.55%;三门县有684株,占总株数的4.36%。
2.1 β多样性的纬度梯度格局
2.1.1 β多样性的相似性及分解
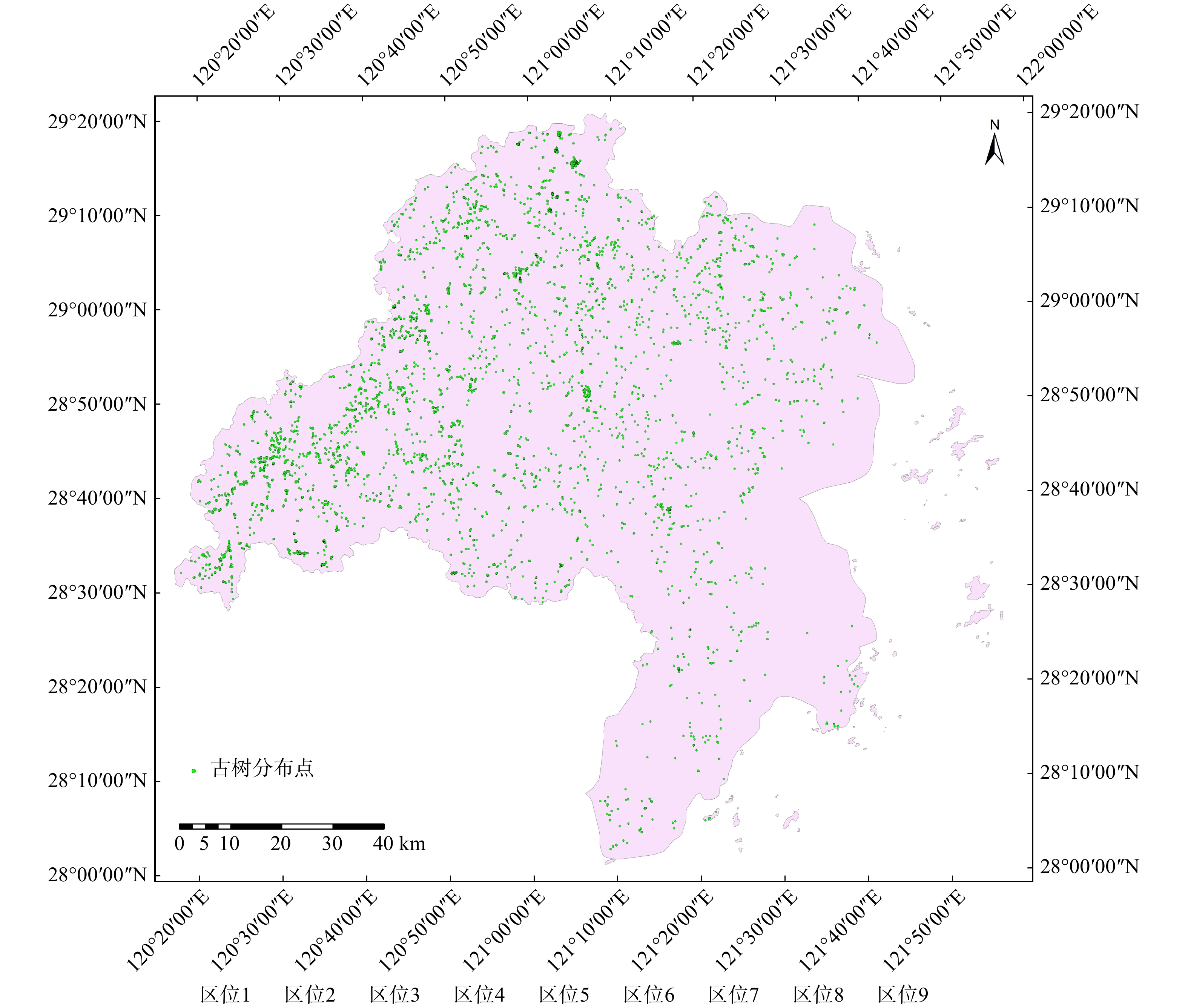
以纬度0°10′作为一个梯度划分单位,共将台州全市划分为8个区位(图1),然后分别统计各区位中古树名木的种类和多度。Sorensen指数法和Jaccard指数法的β多样性沿纬度梯度计算(表1),Bray-Curtis指数法和Morisita-Horn指数法的计算结果见表2。从表1、表2可知,各区位间的相似性程度均不高,无论是Sorensen指数法计算的相似性系数还是Jaccard指数法计算的相似性系数,两区位间相似性最高的是5号和6号区位(Jaccard相似性系数为0.505 9、Sorensen相似性系数为0.671 9,两区位内共有的树种数为43种),两区位间相似性最低的是1号和8号区位(Jaccard系数为0.080 4、Sorensen系数为0.148 8,两区位内共有的树种数为9种)。从公式(1)、(2)可以看出,相似性大小不仅取决于两区位内共有树种数量,还取决于两区位各自所具有的树种数量。按纬度区分的8个区位,两两区位间共有树种数最多的为4号与8号区位,有46种;最少的为1号与2号区位、1号与3号区位,均为5种,但4号区位内有树种83种,8号区位有树种103种;5号和6号区位的指数最大(Bray-Curtis指数为25.031 3,5号区位与6号区位共有树种中多度较少者之和为1 602,Morisita-Horn指数为0.938 1),Bray-Curtis指数最小的为1号和4号区位(0.990 1)、两者共有树种中多度较少者之和为50,Morisita-Horn指数最小的为1号和8号区位(0.013 7),与公式(1)、(2)类似,Bray-Curtis指数大小不仅取决于两区位内共有树种中多度较少者之和,也还取决于两区位各自所具有的树种数,5号区位有树种2 144种,6号区位有2 187种,两两区位间共有树种数中多度较少者之和最多的为5号与6号区位(
1 602 ),最少的为1号与3号区位(35);随着纬度的增加,两相邻区位间的Sorensen指数值、Jaccard指数值、Bray-Curtis指数值和Morisita-Horn指数值随之增加,达到最大值后再随之减少。表 1 按纬度梯度的区位间β多样性二元属性测度结果Table 1. The binary attribute measure of beta diversity by spatial gradient of latitude区位号 1 2 3 4 5 6 7 8 1 0.172 4 0.122 0 0.097 8 0.090 9 0.159 4 0.166 7 0.080 4 2 0.294 1 0.257 1 0.125 0 0.123 3 0.147 1 0.138 9 0.101 9 3 0.217 4 0.409 1 0.233 3 0.189 9 0.200 0 0.236 8 0.139 1 4 0.178 2 0.222 2 0.378 4 0.419 0 0.367 9 0.354 5 0.328 6 5 0.166 7 0.219 5 0.319 1 0.590 6 0.505 9 0.346 9 0.362 9 6 0.275 0 0.256 4 0.333 3 0.537 9 0.671 9 0.422 2 0.375 0 7 0.285 7 0.243 9 0.383 0 0.523 5 0.515 2 0.593 8 0.300 0 8 0.148 8 0.184 9 0.244 3 0.494 6 0.532 5 0.545 5 0.461 5 注:右上角为Jaccard指数,左下角为Sorensen指数。 表 2 按纬度梯度的区位间β多样性数量测度结果Table 2. Quantification of β diversity among locations along latitudinal gradients区位号 1 2 3 4 5 6 7 8 1 2.176 5 1.521 7 0.990 1 1.190 5 1.475 0 1.523 8 1.190 1 2 0.584 0 3.000 0 1.535 4 1.536 6 1.717 9 1.658 5 1.277 3 3 0.472 2 0.804 5 3.819 8 4.170 2 4.377 8 4.319 1 3.022 9 4 0.147 5 0.300 8 0.494 8 17.906 17.227 6 13.946 3 13.688 2 5 0.162 1 0.310 7 0.479 8 0.580 7 25.031 3 20.439 4 13.218 9 6 0.170 4 0.323 0 0.527 7 0.655 5 0.938 1 23.375 0 15.733 3 7 0.143 1 0.264 9 0.423 5 0.613 8 0.834 7 0.869 6 16.023 7 8 0.013 7 0.019 6 0.035 6 0.153 1 0.174 3 0.215 3 0.249 7 注:右上角为Bray-Curtis指数,左下角为Morisita-Horn指数。 沿纬度梯度基于有无二元法的β多样性及其树种轮转组分和树种嵌套组分值见表3、表4。区位总体β多样性(βsor)为0.882 6,树种空间轮转组分(βsim)为0.766 0,树种嵌套组分(βsne)为0.116 5,${\beta }_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}=\dfrac{{\beta }_{\mathrm{s}\mathrm{n}\mathrm{e}}}{{\beta }_{\mathrm{s}\mathrm{o}\mathrm{r}}}= $ $ \dfrac{0.116\;5}{0.882\mathrm{ }6}=0.132\mathrm{ }0 < 0.5 $,表明台州市古树名木沿纬度梯度β多样性主要由树种空间轮转决定[25]。从表3(右上角)可知,区位1与其他区位间的β多样性相异性最大,均大于0.7;其次为区位2,除与区位3的相异性小于0.7外,与其他区位的相异性也都大于0.7;区位间相异性最大的为区位1与区位8(0.851 2),相异性最小的为区位5与区位6(0.328 1)。从表4可知,古树名木的树种空间轮转组分占优势,1号和3号区位、1号和2号区位具有较高的空间轮转组分(0.722 2和0.687 5),2号和8号区位具有较高的树种嵌套组分(0.502 6)。
表 3 沿纬度梯度基于有无二元法和多度的总体β多样性Table 3. The overall β diversity along the latitudinal gradient is based on the presence or absence of binary methods and abundance区位号 1 2 3 4 5 6 7 8 1 0.705 9 0.782 6 0.821 8 0.833 3 0.725 0 0.714 3 0.851 2 2 0.630 0 0.590 9 0.777 8 0.780 5 0.743 6 0.756 1 0.815 1 3 0.791 0 0.591 3 0.621 6 0.680 9 0.666 7 0.617 0 0.755 7 4 0.951 8 0.926 4 0.807 2 0.409 4 0.462 1 0.476 5 0.505 4 5 0.955 6 0.943 7 0.834 8 0.351 5 0.328 1 0.484 8 0.467 5 6 0.948 5 0.941 3 0.836 9 0.399 1 0.260 2 0.406 3 0.454 5 7 0.940 0 0.935 9 0.820 1 0.480 2 0.353 3 0.290 2 0.538 5 8 0.975 6 0.974 2 0.934 3 0.672 3 0.718 8 0.675 0 0.654 1 注:右上角为bsor值,左下角为Btotal值。 沿纬度梯度基于多度的β多样性及树种周转组分和树种多度差异组分值见表3、表5。从表3(左下角)可知,区位1、区位2与其他区位间的β多样性相异性最大;区位间相异性最大的为区位1与区位8(0.975 6),相异性最小的为区位5与区位6(0.260 2)。从表5可知,古树名木的树种多度差异组分占优势,2号和8号区位、1号和8号区位具有极高的树种多度差异组分(0.968 1和0.964 1),1号和2号区位具有较高的树种周转组分(0.57)。
表 4 沿纬度梯度基于有无二元法β多样性的空间轮转组分和嵌套组分Table 4. The spatial rotation component and nested component are based on the diversity of β along the latitudinal gradient with or without binary method区位号 1 2 3 4 5 6 7 8 1 0.687 5 0.722 2 0.500 0 0.611 1 0.388 9 0.333 3 0.500 0 2 0.018 4 0.437 5 0.312 5 0.437 5 0.375 0 0.375 0 0.312 5 3 0.060 4 0.153 4 0.250 0 0.464 3 0.464 3 0.357 1 0.428 6 4 0.321 8 0.465 3 0.371 6 0.333 3 0.371 0 0.409 1 0.445 8 5 0.222 2 0.343 0 0.216 6 0.076 1 0.306 5 0.484 8 0.318 2 6 0.336 1 0.368 6 0.202 4 0.091 1 0.021 7 0.387 1 0.274 2 7 0.381 0 0.381 1 0.259 9 0.067 4 0 0.019 2 0.409 1 8 0.351 2 0.502 6 0.327 2 0.059 6 0.149 3 0.180 4 0.129 4 注:右上角为基于有无二元法的空间轮转组分,左下角为嵌套组分。 表 5 沿纬度梯度基于多度β多样性的空间周转组分和树种多度差异组分Table 5. Spatial turnover components based on multiplicity β diversity and species diversity differences along latitudinal gradients区位号 1 2 3 4 5 6 7 8 1 0.570 0 0.423 9 0.053 9 0.049 8 0.041 0 0.039 4 0.011 5 2 0.060 0 0.173 4 0.017 4 0.027 7 0.023 7 0.024 5 0.006 1 3 0.3672 0.418 0 0.015 5 0.027 8 0.026 5 0.023 0 0.010 3 4 0.8979 0.908 9 0.791 7 0.309 2 0.346 9 0.465 7 0.179 4 5 0.9058 0.916 0 0.807 0 0.042 3 0.250 3 0.325 5 0.258 6 6 0.9075 0.917 6 0.810 4 0.052 2 0.009 9 0.252 4 0.222 6 7 0.9007 0.911 4 0.797 1 0.014 5 0.027 8 0.037 7 0.172 2 8 0.9641 0.968 1 0.92 40 0.492 9 0.460 2 0.452 4 0.481 9 注:右上角为树种周转组分,左下角为树种多度差异组分。 2.1.2 区位与树种对β多样性的贡献度
台州市194种古树名木树种中对沿纬度梯度基于多度的总体β多样性贡献最大的前10个树种依次为:云锦杜鹃、樟、马尾松、柳杉、甜槠、枫香树、苦槠、柏木Cupressus funebris、木荷Schima superba、锥栗Castanea henryi,SCBDj最大值为0.660 5,最小值为0.001 3。8个区位对基于多度的总体β多样性贡献从大到小依次为:8号区位、5号区位、1号区位、2号区位、7号区位、3号区位、6号区位、4号区位,LCCBDi最大值为0.771 3,最小值为0.026 4。
古树名木树种中对沿纬度梯度基于有无二元法的总体β多样性贡献最大的树种依次为:白栎Quercus fabri 、板栗Castanea mollissima、大叶冬青Ilex latifolia 、榧树 Torreya grandis、槐Sophora japonica、金桂Murraya paniculata、榉树Zelkova serrata、雷公鹅耳枥Carpinus viminea、龙柏Sabina chinensis、女贞Ligustrum lucidum、杉木Cunninghamia lanceolata 、甜槠、无患子Sapindus mukorossi、响叶杨Populus adenopoda 、玉兰Magnolia denudata,它们的SCBDj值均为0.008 6。8个区位对基于有无二元法的总体β多样性贡献从大到小依次为:8号区位、4号区位、7号区位、5号区位、1号区位、3号区位、6号区位、2号区位,LCCBDi值最大为0.217 3,最小为0.093 9。
2.2 物种多样性的经度梯度格局
2.2.1 β多样性的相似性及分解
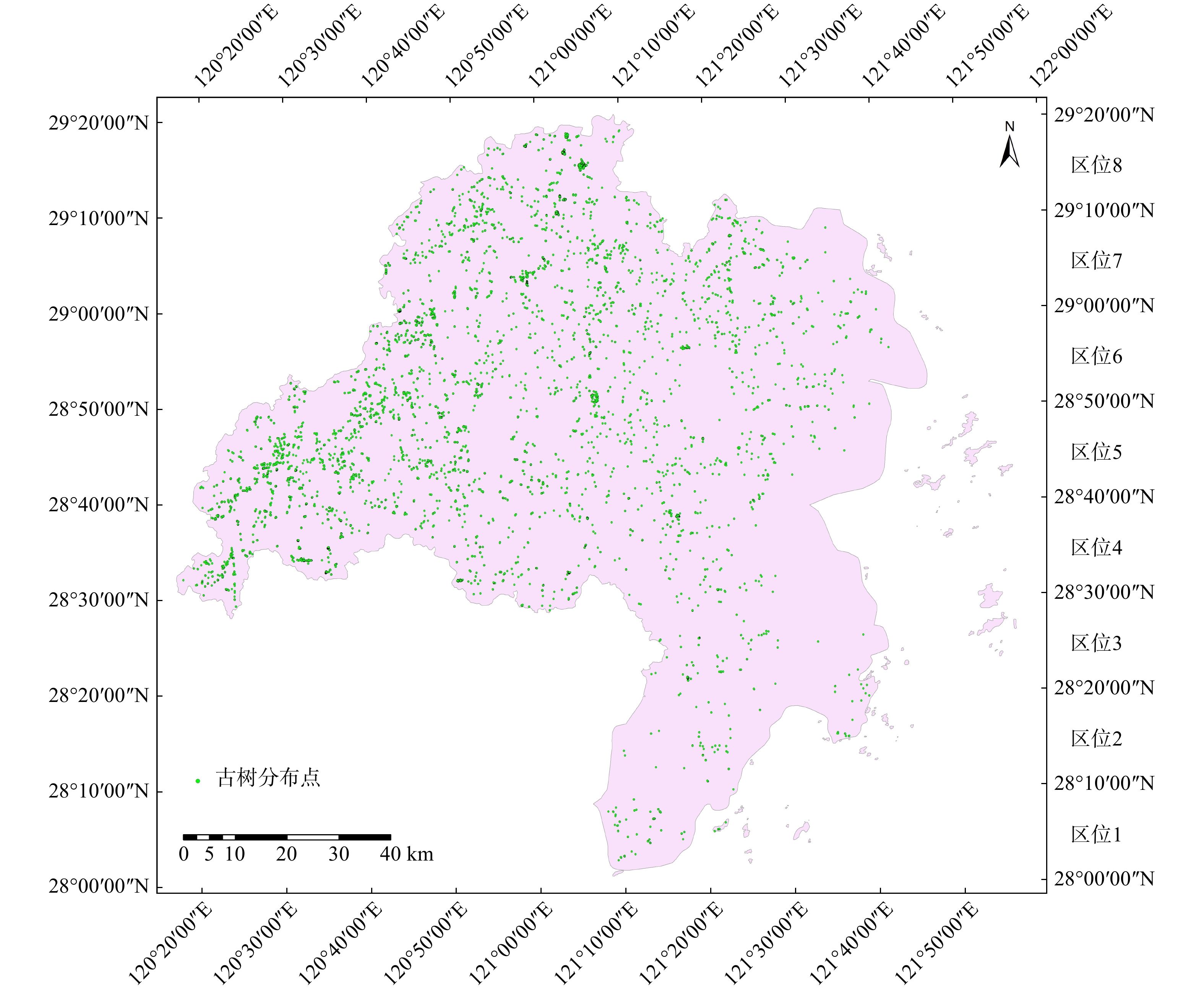
以经度0°10'作为一个梯度划分单位,将台州全市分为9个区位(图2),然后分别统计各区位中古树名木的种类和多度。Sorensen指数法和Jaccard指数法的β多样性沿经度梯度计算结果见表6,Bray-Curtis指数法和Morisita-Horn指数法的计算结果见表7。从表6、表7可知,各区位间的相似性程度均不高,无论是Sorensen指数还是Jaccard指数法计算的相似性系数,两区位间相似性最高的是2号和3号区位(Jaccard相似性系数为0.481 9、Sorensen相似性系数为0.650 4,两区位内共有的树种数为40种),两区位间相似性最低的是5号和9号区位(Jaccard相似性系数为0.033 3,Sorensen相似性系数为0.064 5,两区位内共有的树种数为4种),按经度区分的9个区位,两区位间共有树种数最多的为4号与5号区位,有53种,最少的为2号与9号区位,只有2种,4号区位有树种75种,5号区位有树种120种;对Bray-Curtis指数法和Morisita-Horn指数法而言,3号和4号区位的相似性指数最大(Bray-Curtis指数为22.788 7、3号区位与4号区位共有树种中多度较少者之和为1 618, Morisita-Horn指数为0.968 8),Bray-Curtis指数相似性最小的为2号和9号区位(0.066 7)、两者共有树种中多度较少者之和为2, Morisita-Horn指数最小的为5号和9号区位(0.009 7),两两区位间共有树种数中多度较少者之和最多的为4号与5号区位,为1 914,最少的是2号与9号区位,为2;随着经度的增加,两相邻区位间的Sorensen指数值、Jaccard指数值、Bray-Curtis指数值和Morisita-Horn指数值呈现先小后大的波浪曲线变化趋势。
表 6 按经度梯度的区位间β多样性二元属性测度结果Table 6. Results of pairwise β diversity measures between sites along the longitude gradient区位号 1 2 3 4 5 6 7 8 9 1 0.425 0 0.436 8 0.430 1 0.318 5 0.285 7 0.241 0 0.250 0 0.069 0 2 0.596 5 0.481 9 0.408 6 0.275 4 0.308 6 0.216 9 0.181 8 0.034 5 3 0.608 0 0.650 4 0.434 3 0.335 7 0.329 5 0.258 4 0.186 7 0.044 1 4 0.601 5 0.580 2 0.605 6 0.373 2 0.315 8 0.237 1 0.227 8 0.053 3 5 0.483 1 0.431 8 0.502 7 0.543 6 0.259 3 0.195 7 0.154 5 0.033 3 6 0.444 4 0.471 7 0.495 7 0.480 0 0.411 8 0.376 8 0.263 2 0.058 8 7 0.388 3 0.356 4 0.410 7 0.383 3 0.327 3 0.547 4 0.340 0 0.088 9 8 0.400 0 0.307 7 0.314 6 0.371 1 0.267 6 0.416 7 0.507 5 0.181 8 9 0.129 0 0.066 7 0.084 5 0.101 3 0.064 5 0.111 1 0.163 3 0.307 7 注:右上角为Jaccard指数,左下角为Sorensen指数。 沿经度梯度基于有无二元法的β多样性及其树种轮转组分和树种嵌套组分值见表8、表9。区位总体β多样性(βsor)为0.884 0,树种空间轮转组分(βsim)为0.760 1,树种嵌套组分(βsne)为0.123 9,$ \mathrm{\beta}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}=\dfrac{\mathrm{\beta}_{\mathrm{s}\mathrm{n}\mathrm{e}}}{\mathrm{\beta}_{\mathrm{s}\mathrm{o}\mathrm{r}}}= $ $ \dfrac{0.123\mathrm{ }9}{0.884\mathrm{ }0}=0.140\mathrm{ }2 < 0.5 $,表明台州市古树名木沿经度梯度β多样性主要由树种空间轮转决定[25]。从表8(右上角)可知,区位9与其他区位间的β多样性相异性最大,均大于0.6;其次为区位8,除与区位7、区位6的相异性小于0.6外,与其他区位的相异性也都大于0.6;区位间相异性最大的为区位5与区位9(0.935 5),相异性最小的为区位2与区位3(0.349 6)。从表9可知,8号和9号区位空间轮转组分占优势,其他区位都是嵌套组分占优势;5号和9号区位、6号和9号区位具有较高的空间轮转组分(0.935 5和0.898 7),2号和7号具有较高的树种嵌套组分(0.6)。
表 7 按经度梯度的区位间β多样性数量测度结果Table 7. Measuring the magnitude of β diversity among longitude gradient zones区位号 1 2 3 4 5 6 7 8 9 1 21.684 2 18.592 0 17.097 7 13.910 1 13.333 3 9.728 2 4.275 0 0.193 5 2 0.941 7 22.780 5 20.564 9 17.340 9 12.962 3 10.079 2 4.153 8 0.066 7 3 0.909 3 0.929 3 22.788 7 18.064 2 12.341 9 9.589 3 3.932 6 0.140 8 4 0.888 9 0.891 1 0.968 8 19.630 8 13.072 0 9.366 7 4.288 7 0.151 9 5 0.268 6 0.326 6 0.329 9 0.338 9 11.094 1 7.648 5 3.239 4 0.096 8 6 0.762 3 0.671 2 0.699 8 0.745 1 0.196 4 12.189 5 5.916 7 0.185 2 7 0.784 2 0.650 4 0.716 7 0.754 9 0.159 1 0.819 2 6.835 8 0.244 9 8 0.651 8 0.505 7 0.580 7 0.620 3 0.112 4 0.726 2 0.954 5 0.461 5 9 0.050 6 0.040 9 0.055 7 0.056 9 0.009 7 0.062 9 0.116 3 0.166 4 注:右上角为Bray-Curtis指数,左下角为Morisita-Horn指数。 表 8 沿经度梯度基于有无二元法和多度的总体β多样性Table 8. The overall beta diversity along the longitude gradient is based on the presence or absence of binary method and abundance区位号 1 2 3 4 5 6 7 8 9 1 0.4035 0.392 0 0.3985 0.5169 0.5556 0.6117 0.600 0 0.871 0 2 0.222 9 0.3496 0.4198 0.5682 0.5283 0.6436 0.6923 0.9333 3 0.299 6 0.2363 0.3944 0.4973 0.5043 0.5893 0.6854 0.9155 4 0.362 7 0.3126 0.2022 0.4564 0.520 0 0.6167 0.6289 0.8987 5 0.690 2 0.6342 0.6017 0.5615 0.5882 0.6727 0.7324 0.9355 6 0.443 6 0.5325 0.5306 0.5087 0.7566 0.4526 0.5833 0.8889 7 0.534 6 0.5935 0.5933 0.6112 0.8275 0.394 0 0.4925 0.8367 8 0.793 6 0.8386 0.8368 0.8263 0.9325 0.6989 0.5327 0.6923 9 0.991 6 0.9977 0.9948 0.9944 0.9982 0.9915 0.9839 0.9516 注:右上角为bsor值,左下角为Btotal值。 表 9 沿经度梯度基于有无二元法β多样性的空间轮转组分和嵌套组分Table 9. There are spatial rotation components and nested components based on β diversity with or without binary method along the longitude gradient区位号 1 2 3 4 5 6 7 8 9 1 0.392 9 0.344 8 0.3103 0.2586 0.520 0 0.5556 0.2727 0 2 0.010 7 0.2857 0.3214 0.3214 0.500 0 0.600 0 0.4545 0.50 3 0.047 2 0.0639 0.3582 0.2985 0.420 0 0.4889 0.3636 0.25 4 0.088 2 0.0984 0.0362 0.2933 0.400 0 0.4889 0.1818 0 5 0.258 2 0.2468 0.1988 0.1631 0.300 0 0.400 0 0.1364 0 6 0.035 6 0.0283 0.0843 0.120 0 0.2882 0.4222 0.3182 0.25 7 0.056 1 0.0436 0.1004 0.1278 0.2727 0.0304 0.2273 0 8 0.327 3 0.2378 0.3218 0.447 0 0.596 0 0.2652 0.2653 0 9 0.871 0 0.4333 0.6655 0.8987 0.9355 0.6389 0.8367 0.6923 注:右上角为基于有无二元法的空间轮转组分,左下角为嵌套组分。 沿经度梯度基于多度的β多样性及树种周转组分和树种多度差异组分值见表8、表10。从表8(左下角)可知,区位9、区位8与其它区位间的β多样性相异性最大;区位间相异性最大的为区位5与区位9(0.998 2),相异性最小的为区位3与区位4(0.202 2)。从表10可知,古树名木的树种多度差异组分占优势,5号和9号区位、4号和9号区位具有极高的树种多度差异组分(0.998 2和0.994 4),1号和6号区位具有较高的树种周转组分(0.350 1)。
表 10 沿经度梯度基于多度β多样性的空间周转组分和树种多度差异组分Table 10. Spatial turnover components based on multiplicity β diversity and species diversity difference components along longitude gradient区位号 1 2 3 4 5 6 7 8 9 1 0.1125 0.1525 0.1558 0.0443 0.3501 0.2202 0.0857 0 2 0.110 3 0.199 0 0.2138 0.0575 0.3307 0.1829 0.0797 0.0045 3 0.147 1 0.0373 0.1405 0.0505 0.2932 0.1522 0.0625 0.001 0 4 0.206 8 0.0987 0.0616 0.0548 0.2141 0.1218 0.0284 0 5 0.645 9 0.5767 0.5512 0.5068 0.0594 0.0293 0.0035 0 6 0.093 5 0.2018 0.2373 0.2946 0.6973 0.1664 0.041 0 0.0017 7 0.314 4 0.4105 0.4411 0.4895 0.7982 0.2276 0.0265 0 8 0.707 9 0.759 0 0.7744 0.7979 0.929 0 0.658 0 0.5061 0 9 0.991 6 0.9932 0.9937 0.9944 0.9982 0.9898 0.9839 0.9516 注:右上角为树种周转组分,左下角为树种多度差异组分。 2.2.2 区位与树种对β多样性的贡献度
古树名木树种中对沿经度梯度基于多度的总体β多样性贡献最大的前10个树种依次为:云锦杜鹃、马尾松、柳杉、樟、苦槠、甜槠、枫香树、柏木、木荷、柿Diospyros kaki,SCBDi值最大值为0.699 6,最小值为0.001 4。9个区位对基于多度的总体β多样性贡献从大到小依次为:5号区位、9号区位、8号区位、6号区位、7号区位、4号区位、2号区位、1号区位、3号区位,LCCBDi值最大值为0.784 4,最小值为0.016 1。
古树名木树种中对沿经度梯度基于有无二元法的总体β多样性贡献最大的树种依次为:白栎、侧柏Platycladus orientalis、钩锥Castanopsis tibetana、厚皮香Ternstroemia gymnanthera、黄山松Pinus taiwanensis 、檵木Loropetalum chinense、榉树、蓝果树Nyssa sinensis、麻栎Quercus acutissima、木荷、女贞、沙梨Pyrus pyrifolia、杉木、苏铁Cycas revoluta 、甜槠、乌桕Sapium sebiferum、响叶杨Populus adenopoda 、野柿Diospyros kaki. var. silvestris、柞木Xylosma racemosum、重阳木Bischofia polycarpa、锥栗、紫藤Wisteria sinensis,它们的SCBDj值均为0.008 7。9个区位对基于有无二元法的总体β多样性贡献从大到小依次为:5号区位、4号区位、7号区位、3号区位、2号区位、6号区位、9号区位、1号区位、8号区位,LCCBDi值最大值为0.237 4,最小值为0.071 1。
2.3 物种多样性的海拔梯度格局
2.3.1 β多样性的相似性及分解
以海拔每升高100 m作为一个梯度划分单位,台州全市可以划分为11个区位,然后分别统计各区位中古树名木的种类和多度。Sorensen指数法和Jaccard指数法的β多样性海拔梯度计算结果见表11,Bray-Curtis指数法和Morisita-Horn指数法的计算结果见表12。从表11、表12可知,各区位间的相似性程度均不高,无论是Sorensen指数法计算的相似性系数还是Jaccard指数法计算的相似性系数,两区位间相似性最高的是7号和8号区位(Jaccard相似性系数为0.5、Sorensen相似性系数为0.666 7,两区位内共有的树种数为33种),两区位间相似性最低的是5号和11号区位(Jaccard相似性系数为0.011 2、Sorensen相似性系数为0.022 2,两区位内共有的树种数为1种),按海拔区分的11个区位,两两区位间共有树种数最多的为4号与5号、5号与6号区位,均有树种46种,最少的为1号与11号、2号与11号、3号与11号、4号与11号、5号与11号区位, 均为1种,4号区位有树种62种,5号区位有树种84种,6号区位有树种69种;10号和11号区位的Bray-Curtis指数最大(48.421 1),两者共有树种中多度较少者之和为920, 3号和4号区位的Morisita-Horn指数最大(0.938 1),Bray-Curtis指数最小的为2号和11号区位(0.026)、两者共有树种中多度较少者之和为1,两两区位间共有树种数中多度较少者之和最多的为1号与2号区位,为1 811,最少的为2号与11号、3号与11号区位,均为1,Morisita-Horn指数最小值为0,具体为2号和11号区位、3号和11号区位、4号和11号区位;随着海拔的增加,两相邻区位间的Sorensen指数值、Jaccard指数值、Bray-Curtis指数值和Morisita-Horn指数值呈先大后小的波浪曲线变化的趋势。
表 11 按海拔梯度的区位间β多样性二元属性测度结果Table 11. Binary attribute measurement of inter-plot β diversity according to altitude gradient区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.4455 0.2828 0.3173 0.2927 0.2632 0.2475 0.1739 0.0625 0.0594 0.0125 2 0.616 4 0.382 0 0.3854 0.3478 0.3084 0.3118 0.2235 0.1011 0.0729 0.0132 3 0.440 9 0.5528 0.4074 0.360 0 0.3444 0.3038 0.2143 0.1127 0.0909 0.0175 4 0.481 8 0.5564 0.5789 0.460 0 0.3505 0.2841 0.2179 0.0854 0.0682 0.0149 5 0.452 8 0.5161 0.5294 0.6301 0.4299 0.2857 0.2188 0.1212 0.1048 0.0112 6 0.416 7 0.4714 0.5124 0.5191 0.6013 0.3793 0.2911 0.1707 0.1477 0.0274 7 0.396 8 0.4754 0.466 0 0.4425 0.4444 0.550 0 0.500 0 0.2188 0.1857 0.0556 8 0.296 3 0.3654 0.3529 0.3579 0.359 0.451 0 0.6667 0.3333 0.250 0 0.1143 9 0.117 6 0.1837 0.2025 0.1573 0.2162 0.2917 0.359 0.500 0 0.3409 0.1379 10 0.112 1 0.1359 0.1667 0.1277 0.1897 0.2574 0.3133 0.400 0 0.5085 0.1875 11 0.024 7 0.026 0 0.0345 0.0294 0.0222 0.0533 0.1053 0.2051 0.2424 0.3158 注:右上角为Jaccard指数,左下角为Sorensen指数。 表 12 按海拔梯度的区位间β多样性数量测度结果Table 12. Quantitative measurement of inter-plot β diversity according to elevation gradient区位号 1 2 3 4 5 6 7 8 9 10 11 1 24.8082 13.3386 12.073 0 8.6541 7.0694 6.8889 1.9444 0.8039 0.6168 0.3951 2 0.824 4 16.6341 14.6165 17.3032 10.2714 9.1311 2.1538 0.7347 0.4466 0.026 0 3 0.418 3 0.6889 16.4035 13.0294 12.0165 10.5437 2.8235 0.8861 0.5476 0.0345 4 0.283 8 0.5177 0.9294 12.5205 10.5954 10.5133 2.6316 0.8539 0.5532 0.1471 5 0.162 1 0.5204 0.7995 0.761 0 15.0327 10.0741 3.094 0 1.0811 0.8276 0.400 0 6 0.079 5 0.3141 0.6504 0.691 0 0.8829 11.400 0 4.6275 2.1875 1.8416 0.7467 7 0.075 4 0.3403 0.7093 0.814 0 0.8148 0.7914 7.0952 3.0513 3.4458 1.0175 8 0.021 6 0.0715 0.2065 0.2707 0.2657 0.4301 0.5454 4.000 0 5.0769 1.5385 9 0.011 5 0.0178 0.0808 0.1338 0.0645 0.1717 0.3072 0.8155 3.661 0 1.8182 10 0.004 0 0.0023 0.0016 0.0029 0.0057 0.0182 0.0337 0.0593 0.0452 48.4211 11 0.0001 0 0 0 0.0001 0.0004 0.0007 0.0013 0.0014 0.5171 注:右上角为Bray-Curtis指数,左下角为Morisita-Horn指数。 沿海拔梯度基于有无二元法的β多样性及其树种轮转组分和树种嵌套组分值见表13、表14。区位总体β多样性(βsor)为0.905 5,树种空间轮转组分(βsim)为0.842 1,树种嵌套组分(βsne)为0.063 4,$ \mathrm{\beta}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}=\dfrac{\mathrm{\beta}_{\mathrm{s}\mathrm{n}\mathrm{e}}}{\mathrm{\beta}_{\mathrm{s}\mathrm{o}\mathrm{r}}}= $ $ \dfrac{0.063\mathrm{ }4}{0.905\mathrm{ }5}=0.07 < 0.5 $,表明台州市古树名木沿海拔梯度β多样性主要由树种空间轮转决定[25]。从表13(右上角)可知,区位11与其他区位间的β多样性相异性最大,均大于0.6;其次为区位10,除与区位9的相异性小于0.6外,与其它区位的相异性也都大于0.6;区位间相异性最大的为区位11与区位5(0.977 8),相异性最小的为区位7与区位8(0.333 3)。从表14可知,古树名木的树种空间轮转组分占优势,1号和11号区位、2号和11号区位、3号和11号区位、4号和11号区位、5号和11号区位具有较高的空间轮转组分(均为0.833 3),10号和11号具有较高的树种嵌套组分(0.684 2)。
表 13 沿海拔梯度基于有无二元法和多度的总体β多样性Table 13. The overall β diversity along the elevation gradient is based on the presence or absence of binary methods and abundance区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.383 6 0.5591 0.5182 0.5472 0.5833 0.6032 0.7037 0.8824 0.8879 0.9753 2 0.388 7 0.4472 0.4436 0.4839 0.5286 0.5246 0.6346 0.8163 0.8641 0.974 0 3 0.613 7 0.4765 0.4211 0.4706 0.4876 0.534 0 0.6471 0.7975 0.8333 0.9655 4 0.619 9 0.4982 0.1988 0.3699 0.4809 0.5575 0.6421 0.8427 0.8723 0.9706 5 0.732 3 0.425 0 0.4328 0.4084 0.3987 0.5556 0.641 0 0.7838 0.8103 0.9778 6 0.775 2 0.645 0 0.4209 0.4396 0.296 0 0.450 0 0.549 0 0.7083 0.7426 0.9467 7 0.787 1 0.6906 0.4728 0.4136 0.517 0 0.379 0 0.3333 0.641 0 0.6867 0.8947 8 0.941 0 0.9274 0.8446 0.8344 0.8426 0.7202 0.5178 0.500 0 0.600 0 0.7949 9 0.975 5 0.975 0 0.9476 0.9416 0.9426 0.8579 0.7683 0.5303 0.4915 0.7576 10 0.987 6 0.9905 0.9862 0.9842 0.9765 0.9464 0.9052 0.868 0 0.9057 0.6842 11 0.992 2 0.9995 0.999 0 0.9952 0.9874 0.9751 0.9677 0.9531 0.944 0 0.3987 注:右上角为bsor值,左下角为Btotal值。 表 14 沿海拔梯度基于有无二元法β多样性的空间轮转组分和嵌套组分Table 14. There are spatial rotation components and nested components based on β diversity with or without binary method along elevation gradients区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.3662 0.4615 0.4677 0.520 0 0.5652 0.5098 0.5152 0.7778 0.8125 0.8333 2 0.017 4 0.3462 0.4032 0.4366 0.5217 0.4314 0.4242 0.6667 0.7813 0.8333 3 0.097 5 0.101 0 0.3654 0.3077 0.4038 0.5294 0.5455 0.7037 0.7813 0.8333 4 0.050 5 0.0404 0.0557 0.2581 0.4516 0.5098 0.4848 0.7407 0.8125 0.8333 5 0.027 2 0.0473 0.1629 0.1118 0.3333 0.4118 0.3636 0.5556 0.6563 0.8333 6 0.018 1 0.0068 0.0838 0.0293 0.0654 0.3529 0.303 0 0.4815 0.5938 0.6667 7 0.093 4 0.0932 0.0046 0.0477 0.1438 0.0971 0.1515 0.4815 0.5938 0.500 0 8 0.188 6 0.2104 0.1016 0.1573 0.2774 0.246 0 0.1818 0.4444 0.5938 0.3333 9 0.104 6 0.1497 0.0938 0.102 0 0.2282 0.2269 0.1595 0.0556 0.4444 0.3333 10 0.075 4 0.0828 0.0521 0.0598 0.1541 0.1488 0.093 0 0.0063 0.0471 0 11 0.142 0 0.1407 0.1322 0.1373 0.1444 0.280 0 0.3947 0.4615 0.4242 0.6842 注:右上角为基于有无二元法的空间轮转组分,左下角为嵌套组分。 沿海拔梯度基于多度的β多样性及树种周转组分和树种多度差异组分值见表13、表15。从表13(左下角)可知,区位10、区位11与其他区位间的β多样性相异性最大;区位间相异性最大的为区位2与区位11(0.999 5),相异性最小的为区位3与区位4(0.198 8)。从表15可知,除10号和11号区位外,其余区位的古树名木树种多度差异组分占优势,1号和9号区位、2号和9号区位具有极高的树种多度差异组分(0.909 9和0.895),7号和11号具有极高的树种周转组分(0.943 2)。
表 15 沿海拔梯度基于多度β多样性的空间周转组分和树种多度差异组分Table 15. Spatial turnover components based on multiplicity β diversity and species diversity differences along altitude gradients区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.3082 0.1537 0.1485 0.4871 0.3613 0.2168 0.1432 0.0656 0.789 0.4387 2 0.0805 0.0824 0.0919 0.2569 0.3002 0.1772 0.1608 0.080 0 0.8705 0.5044 3 0.460 0 0.3941 0.1842 0.1908 0.364 0 0.3233 0.3109 0.1738 0.6986 0.8736 4 0.4714 0.4063 0.0146 0.1528 0.3682 0.2784 0.3113 0.1737 0.6833 0.8841 5 0.2453 0.1681 0.242 0 0.2557 0.1084 0.1392 0.1557 0.087 0.9275 0.6308 6 0.4139 0.3449 0.0569 0.0715 0.1876 0.1743 0.147 0 0.0622 0.7119 0.7939 7 0.5703 0.5133 0.1495 0.1352 0.3778 0.2047 0.1003 0.0623 0.4861 0.9432 8 0.7978 0.7665 0.5337 0.5232 0.687 0 0.5732 0.4175 0.1213 0.156 0 0.5156 9 0.9099 0.895 0 0.7738 0.7679 0.8556 0.7957 0.7059 0.409 0 0.0375 0.226 0 10 0.1987 0.1201 0.2876 0.3009 0.049 0 0.2345 0.4191 0.712 0 0.8682 0 11 0.5535 0.4951 0.1255 0.1111 0.3566 0.1811 0.0245 0.4375 0.718 0 0.3987 注:右上角为树种周转组分,左下角为树种多度差异组分。 2.3.2 区位与树种对β多样性的贡献度
古树名木树种中对沿海拔梯度基于多度的总体β多样性贡献最大的前10个树种依次为:樟、云锦杜鹃、马尾松、柳杉、苦槠、枫香树、甜槠、柏木、朴树Celtis sinensis 、银杏Ginkgo biloba ,SCBDi最大值为0.449 8,最小值为0.001 8。11个区位对基于多度的总体β多样性贡献从大到小依次为:1号区位、10号区位、2号区位、11号区位、5号区位、9号区位、8号区位、6号区位、7号区位、4号区位、3号区位,LCCBDi最大值为0.322 6,最小值为0.010 3。
古树名木树种中对沿海拔梯度基于有无二元法的总体β多样性贡献最大的树种依次为:板栗、糙叶树Aphananthe aspera、槐树、黄山松、蓝果树、杉木、钩栗、红楠Machilus thunbergii 、金桂、榉树、罗汉松Podocarpus macrophyllus、麻栎、七子花Heptacodium miconioides、乌桕、杨梅Myrica rubra、圆柏Sabina chinensis,它们的SCBDj值均为0.008 5。11个区位对基于有无二元法的总体β多样性贡献从大到小依次为:1号区位、5号区位、2号区位、6号区位、10号区位、4号区位、9号区位、3号区位、7号区位、11号区位、8号区位,LCCBDi最大值为0.131 7,最小值为0.055 7。
综上,台州市古树名木各树种中株数居前10位的是樟(3 026株)、云锦杜鹃(2 214株)、马尾松(1 928株)、枫香树(1 463株)、苦槠(1 325株)、柳杉(1 013株)、甜槠(651株)、柏木(617株)、青冈栎Quercus glauca(281株)、朴树(265株)。除青冈栎和朴树外的前8个树种,无论是对沿纬度梯度还是沿经度梯度或沿海拔梯度基于多度的总体β多样性贡献最大,主要原因是这8个树种在全市分布较为普遍且集中。对基于有无二元法的总体β多样性贡献大的树种中,除甜槠、木荷、榧树和糙叶树4个树种的株数达到上百株外,其余各树种只有几株或几十株,但它们的分布比较均匀,这就是它们无论是对沿纬度梯度还是沿经度梯度或沿海拔梯度基于有无二元法的总体β多样性贡献大的原因。
3. 小结与讨论
台州全市共有古树名木15 668株,其中古树15 654株、名木14株,隶属于56科、117属、194种[10],古树名木株数最多的前10种树种由多到少依次为:樟、云锦杜鹃、马尾松、枫香树、苦槠、柳杉、甜槠、柏木、青冈栎、朴树,其中前8个树种对基于多度的总体β多样性贡献,无论沿纬度梯度还是沿经度梯度或者沿海拔梯度,都是最大的;对基于有无二元法的总体β多样性贡献大的树种中,除甜槠、木荷、榧树和糙叶树4个树种的株数达到上百株外,其余各树种的株数只有几株或几十株,但它们在台州全市的分布比较均匀。此外,还有48种古树名木树种中株数只有1株,少于等于10株的有140种,故在选择β多样性指数时,不能仅考虑测度方法的简便易用,还需考虑稀疏种在区位中的作用被夸大[15],如本研究中在确定古树名木树种、区位对总体β多样性的贡献时,无论是沿纬度梯度还是沿经度梯度或者沿海拔梯度方向,基于有无二元法与基于多度的研究结果都不一样。
台州市具有极为丰富的乡土树种资源,据最新研究结果,全市有乡土树种998种,隶属93科、325属[26],现有的古树名木为56科、117属、194种。因此,既要对现有的古树名木资源积极地采取因树施策的保护措施,又要对一些景观价值高、寿命长、具有科学或纪念意义的优秀乡土树种,尤其是那些稀有的树种,加强后备资源的培育管理,不断地增加和丰富全市古树名木资源的多样性。
-
表 1 按纬度梯度的区位间β多样性二元属性测度结果
Table 1 The binary attribute measure of beta diversity by spatial gradient of latitude
区位号 1 2 3 4 5 6 7 8 1 0.172 4 0.122 0 0.097 8 0.090 9 0.159 4 0.166 7 0.080 4 2 0.294 1 0.257 1 0.125 0 0.123 3 0.147 1 0.138 9 0.101 9 3 0.217 4 0.409 1 0.233 3 0.189 9 0.200 0 0.236 8 0.139 1 4 0.178 2 0.222 2 0.378 4 0.419 0 0.367 9 0.354 5 0.328 6 5 0.166 7 0.219 5 0.319 1 0.590 6 0.505 9 0.346 9 0.362 9 6 0.275 0 0.256 4 0.333 3 0.537 9 0.671 9 0.422 2 0.375 0 7 0.285 7 0.243 9 0.383 0 0.523 5 0.515 2 0.593 8 0.300 0 8 0.148 8 0.184 9 0.244 3 0.494 6 0.532 5 0.545 5 0.461 5 注:右上角为Jaccard指数,左下角为Sorensen指数。 表 2 按纬度梯度的区位间β多样性数量测度结果
Table 2 Quantification of β diversity among locations along latitudinal gradients
区位号 1 2 3 4 5 6 7 8 1 2.176 5 1.521 7 0.990 1 1.190 5 1.475 0 1.523 8 1.190 1 2 0.584 0 3.000 0 1.535 4 1.536 6 1.717 9 1.658 5 1.277 3 3 0.472 2 0.804 5 3.819 8 4.170 2 4.377 8 4.319 1 3.022 9 4 0.147 5 0.300 8 0.494 8 17.906 17.227 6 13.946 3 13.688 2 5 0.162 1 0.310 7 0.479 8 0.580 7 25.031 3 20.439 4 13.218 9 6 0.170 4 0.323 0 0.527 7 0.655 5 0.938 1 23.375 0 15.733 3 7 0.143 1 0.264 9 0.423 5 0.613 8 0.834 7 0.869 6 16.023 7 8 0.013 7 0.019 6 0.035 6 0.153 1 0.174 3 0.215 3 0.249 7 注:右上角为Bray-Curtis指数,左下角为Morisita-Horn指数。 表 3 沿纬度梯度基于有无二元法和多度的总体β多样性
Table 3 The overall β diversity along the latitudinal gradient is based on the presence or absence of binary methods and abundance
区位号 1 2 3 4 5 6 7 8 1 0.705 9 0.782 6 0.821 8 0.833 3 0.725 0 0.714 3 0.851 2 2 0.630 0 0.590 9 0.777 8 0.780 5 0.743 6 0.756 1 0.815 1 3 0.791 0 0.591 3 0.621 6 0.680 9 0.666 7 0.617 0 0.755 7 4 0.951 8 0.926 4 0.807 2 0.409 4 0.462 1 0.476 5 0.505 4 5 0.955 6 0.943 7 0.834 8 0.351 5 0.328 1 0.484 8 0.467 5 6 0.948 5 0.941 3 0.836 9 0.399 1 0.260 2 0.406 3 0.454 5 7 0.940 0 0.935 9 0.820 1 0.480 2 0.353 3 0.290 2 0.538 5 8 0.975 6 0.974 2 0.934 3 0.672 3 0.718 8 0.675 0 0.654 1 注:右上角为bsor值,左下角为Btotal值。 表 4 沿纬度梯度基于有无二元法β多样性的空间轮转组分和嵌套组分
Table 4 The spatial rotation component and nested component are based on the diversity of β along the latitudinal gradient with or without binary method
区位号 1 2 3 4 5 6 7 8 1 0.687 5 0.722 2 0.500 0 0.611 1 0.388 9 0.333 3 0.500 0 2 0.018 4 0.437 5 0.312 5 0.437 5 0.375 0 0.375 0 0.312 5 3 0.060 4 0.153 4 0.250 0 0.464 3 0.464 3 0.357 1 0.428 6 4 0.321 8 0.465 3 0.371 6 0.333 3 0.371 0 0.409 1 0.445 8 5 0.222 2 0.343 0 0.216 6 0.076 1 0.306 5 0.484 8 0.318 2 6 0.336 1 0.368 6 0.202 4 0.091 1 0.021 7 0.387 1 0.274 2 7 0.381 0 0.381 1 0.259 9 0.067 4 0 0.019 2 0.409 1 8 0.351 2 0.502 6 0.327 2 0.059 6 0.149 3 0.180 4 0.129 4 注:右上角为基于有无二元法的空间轮转组分,左下角为嵌套组分。 表 5 沿纬度梯度基于多度β多样性的空间周转组分和树种多度差异组分
Table 5 Spatial turnover components based on multiplicity β diversity and species diversity differences along latitudinal gradients
区位号 1 2 3 4 5 6 7 8 1 0.570 0 0.423 9 0.053 9 0.049 8 0.041 0 0.039 4 0.011 5 2 0.060 0 0.173 4 0.017 4 0.027 7 0.023 7 0.024 5 0.006 1 3 0.3672 0.418 0 0.015 5 0.027 8 0.026 5 0.023 0 0.010 3 4 0.8979 0.908 9 0.791 7 0.309 2 0.346 9 0.465 7 0.179 4 5 0.9058 0.916 0 0.807 0 0.042 3 0.250 3 0.325 5 0.258 6 6 0.9075 0.917 6 0.810 4 0.052 2 0.009 9 0.252 4 0.222 6 7 0.9007 0.911 4 0.797 1 0.014 5 0.027 8 0.037 7 0.172 2 8 0.9641 0.968 1 0.92 40 0.492 9 0.460 2 0.452 4 0.481 9 注:右上角为树种周转组分,左下角为树种多度差异组分。 表 6 按经度梯度的区位间β多样性二元属性测度结果
Table 6 Results of pairwise β diversity measures between sites along the longitude gradient
区位号 1 2 3 4 5 6 7 8 9 1 0.425 0 0.436 8 0.430 1 0.318 5 0.285 7 0.241 0 0.250 0 0.069 0 2 0.596 5 0.481 9 0.408 6 0.275 4 0.308 6 0.216 9 0.181 8 0.034 5 3 0.608 0 0.650 4 0.434 3 0.335 7 0.329 5 0.258 4 0.186 7 0.044 1 4 0.601 5 0.580 2 0.605 6 0.373 2 0.315 8 0.237 1 0.227 8 0.053 3 5 0.483 1 0.431 8 0.502 7 0.543 6 0.259 3 0.195 7 0.154 5 0.033 3 6 0.444 4 0.471 7 0.495 7 0.480 0 0.411 8 0.376 8 0.263 2 0.058 8 7 0.388 3 0.356 4 0.410 7 0.383 3 0.327 3 0.547 4 0.340 0 0.088 9 8 0.400 0 0.307 7 0.314 6 0.371 1 0.267 6 0.416 7 0.507 5 0.181 8 9 0.129 0 0.066 7 0.084 5 0.101 3 0.064 5 0.111 1 0.163 3 0.307 7 注:右上角为Jaccard指数,左下角为Sorensen指数。 表 7 按经度梯度的区位间β多样性数量测度结果
Table 7 Measuring the magnitude of β diversity among longitude gradient zones
区位号 1 2 3 4 5 6 7 8 9 1 21.684 2 18.592 0 17.097 7 13.910 1 13.333 3 9.728 2 4.275 0 0.193 5 2 0.941 7 22.780 5 20.564 9 17.340 9 12.962 3 10.079 2 4.153 8 0.066 7 3 0.909 3 0.929 3 22.788 7 18.064 2 12.341 9 9.589 3 3.932 6 0.140 8 4 0.888 9 0.891 1 0.968 8 19.630 8 13.072 0 9.366 7 4.288 7 0.151 9 5 0.268 6 0.326 6 0.329 9 0.338 9 11.094 1 7.648 5 3.239 4 0.096 8 6 0.762 3 0.671 2 0.699 8 0.745 1 0.196 4 12.189 5 5.916 7 0.185 2 7 0.784 2 0.650 4 0.716 7 0.754 9 0.159 1 0.819 2 6.835 8 0.244 9 8 0.651 8 0.505 7 0.580 7 0.620 3 0.112 4 0.726 2 0.954 5 0.461 5 9 0.050 6 0.040 9 0.055 7 0.056 9 0.009 7 0.062 9 0.116 3 0.166 4 注:右上角为Bray-Curtis指数,左下角为Morisita-Horn指数。 表 8 沿经度梯度基于有无二元法和多度的总体β多样性
Table 8 The overall beta diversity along the longitude gradient is based on the presence or absence of binary method and abundance
区位号 1 2 3 4 5 6 7 8 9 1 0.4035 0.392 0 0.3985 0.5169 0.5556 0.6117 0.600 0 0.871 0 2 0.222 9 0.3496 0.4198 0.5682 0.5283 0.6436 0.6923 0.9333 3 0.299 6 0.2363 0.3944 0.4973 0.5043 0.5893 0.6854 0.9155 4 0.362 7 0.3126 0.2022 0.4564 0.520 0 0.6167 0.6289 0.8987 5 0.690 2 0.6342 0.6017 0.5615 0.5882 0.6727 0.7324 0.9355 6 0.443 6 0.5325 0.5306 0.5087 0.7566 0.4526 0.5833 0.8889 7 0.534 6 0.5935 0.5933 0.6112 0.8275 0.394 0 0.4925 0.8367 8 0.793 6 0.8386 0.8368 0.8263 0.9325 0.6989 0.5327 0.6923 9 0.991 6 0.9977 0.9948 0.9944 0.9982 0.9915 0.9839 0.9516 注:右上角为bsor值,左下角为Btotal值。 表 9 沿经度梯度基于有无二元法β多样性的空间轮转组分和嵌套组分
Table 9 There are spatial rotation components and nested components based on β diversity with or without binary method along the longitude gradient
区位号 1 2 3 4 5 6 7 8 9 1 0.392 9 0.344 8 0.3103 0.2586 0.520 0 0.5556 0.2727 0 2 0.010 7 0.2857 0.3214 0.3214 0.500 0 0.600 0 0.4545 0.50 3 0.047 2 0.0639 0.3582 0.2985 0.420 0 0.4889 0.3636 0.25 4 0.088 2 0.0984 0.0362 0.2933 0.400 0 0.4889 0.1818 0 5 0.258 2 0.2468 0.1988 0.1631 0.300 0 0.400 0 0.1364 0 6 0.035 6 0.0283 0.0843 0.120 0 0.2882 0.4222 0.3182 0.25 7 0.056 1 0.0436 0.1004 0.1278 0.2727 0.0304 0.2273 0 8 0.327 3 0.2378 0.3218 0.447 0 0.596 0 0.2652 0.2653 0 9 0.871 0 0.4333 0.6655 0.8987 0.9355 0.6389 0.8367 0.6923 注:右上角为基于有无二元法的空间轮转组分,左下角为嵌套组分。 表 10 沿经度梯度基于多度β多样性的空间周转组分和树种多度差异组分
Table 10 Spatial turnover components based on multiplicity β diversity and species diversity difference components along longitude gradient
区位号 1 2 3 4 5 6 7 8 9 1 0.1125 0.1525 0.1558 0.0443 0.3501 0.2202 0.0857 0 2 0.110 3 0.199 0 0.2138 0.0575 0.3307 0.1829 0.0797 0.0045 3 0.147 1 0.0373 0.1405 0.0505 0.2932 0.1522 0.0625 0.001 0 4 0.206 8 0.0987 0.0616 0.0548 0.2141 0.1218 0.0284 0 5 0.645 9 0.5767 0.5512 0.5068 0.0594 0.0293 0.0035 0 6 0.093 5 0.2018 0.2373 0.2946 0.6973 0.1664 0.041 0 0.0017 7 0.314 4 0.4105 0.4411 0.4895 0.7982 0.2276 0.0265 0 8 0.707 9 0.759 0 0.7744 0.7979 0.929 0 0.658 0 0.5061 0 9 0.991 6 0.9932 0.9937 0.9944 0.9982 0.9898 0.9839 0.9516 注:右上角为树种周转组分,左下角为树种多度差异组分。 表 11 按海拔梯度的区位间β多样性二元属性测度结果
Table 11 Binary attribute measurement of inter-plot β diversity according to altitude gradient
区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.4455 0.2828 0.3173 0.2927 0.2632 0.2475 0.1739 0.0625 0.0594 0.0125 2 0.616 4 0.382 0 0.3854 0.3478 0.3084 0.3118 0.2235 0.1011 0.0729 0.0132 3 0.440 9 0.5528 0.4074 0.360 0 0.3444 0.3038 0.2143 0.1127 0.0909 0.0175 4 0.481 8 0.5564 0.5789 0.460 0 0.3505 0.2841 0.2179 0.0854 0.0682 0.0149 5 0.452 8 0.5161 0.5294 0.6301 0.4299 0.2857 0.2188 0.1212 0.1048 0.0112 6 0.416 7 0.4714 0.5124 0.5191 0.6013 0.3793 0.2911 0.1707 0.1477 0.0274 7 0.396 8 0.4754 0.466 0 0.4425 0.4444 0.550 0 0.500 0 0.2188 0.1857 0.0556 8 0.296 3 0.3654 0.3529 0.3579 0.359 0.451 0 0.6667 0.3333 0.250 0 0.1143 9 0.117 6 0.1837 0.2025 0.1573 0.2162 0.2917 0.359 0.500 0 0.3409 0.1379 10 0.112 1 0.1359 0.1667 0.1277 0.1897 0.2574 0.3133 0.400 0 0.5085 0.1875 11 0.024 7 0.026 0 0.0345 0.0294 0.0222 0.0533 0.1053 0.2051 0.2424 0.3158 注:右上角为Jaccard指数,左下角为Sorensen指数。 表 12 按海拔梯度的区位间β多样性数量测度结果
Table 12 Quantitative measurement of inter-plot β diversity according to elevation gradient
区位号 1 2 3 4 5 6 7 8 9 10 11 1 24.8082 13.3386 12.073 0 8.6541 7.0694 6.8889 1.9444 0.8039 0.6168 0.3951 2 0.824 4 16.6341 14.6165 17.3032 10.2714 9.1311 2.1538 0.7347 0.4466 0.026 0 3 0.418 3 0.6889 16.4035 13.0294 12.0165 10.5437 2.8235 0.8861 0.5476 0.0345 4 0.283 8 0.5177 0.9294 12.5205 10.5954 10.5133 2.6316 0.8539 0.5532 0.1471 5 0.162 1 0.5204 0.7995 0.761 0 15.0327 10.0741 3.094 0 1.0811 0.8276 0.400 0 6 0.079 5 0.3141 0.6504 0.691 0 0.8829 11.400 0 4.6275 2.1875 1.8416 0.7467 7 0.075 4 0.3403 0.7093 0.814 0 0.8148 0.7914 7.0952 3.0513 3.4458 1.0175 8 0.021 6 0.0715 0.2065 0.2707 0.2657 0.4301 0.5454 4.000 0 5.0769 1.5385 9 0.011 5 0.0178 0.0808 0.1338 0.0645 0.1717 0.3072 0.8155 3.661 0 1.8182 10 0.004 0 0.0023 0.0016 0.0029 0.0057 0.0182 0.0337 0.0593 0.0452 48.4211 11 0.0001 0 0 0 0.0001 0.0004 0.0007 0.0013 0.0014 0.5171 注:右上角为Bray-Curtis指数,左下角为Morisita-Horn指数。 表 13 沿海拔梯度基于有无二元法和多度的总体β多样性
Table 13 The overall β diversity along the elevation gradient is based on the presence or absence of binary methods and abundance
区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.383 6 0.5591 0.5182 0.5472 0.5833 0.6032 0.7037 0.8824 0.8879 0.9753 2 0.388 7 0.4472 0.4436 0.4839 0.5286 0.5246 0.6346 0.8163 0.8641 0.974 0 3 0.613 7 0.4765 0.4211 0.4706 0.4876 0.534 0 0.6471 0.7975 0.8333 0.9655 4 0.619 9 0.4982 0.1988 0.3699 0.4809 0.5575 0.6421 0.8427 0.8723 0.9706 5 0.732 3 0.425 0 0.4328 0.4084 0.3987 0.5556 0.641 0 0.7838 0.8103 0.9778 6 0.775 2 0.645 0 0.4209 0.4396 0.296 0 0.450 0 0.549 0 0.7083 0.7426 0.9467 7 0.787 1 0.6906 0.4728 0.4136 0.517 0 0.379 0 0.3333 0.641 0 0.6867 0.8947 8 0.941 0 0.9274 0.8446 0.8344 0.8426 0.7202 0.5178 0.500 0 0.600 0 0.7949 9 0.975 5 0.975 0 0.9476 0.9416 0.9426 0.8579 0.7683 0.5303 0.4915 0.7576 10 0.987 6 0.9905 0.9862 0.9842 0.9765 0.9464 0.9052 0.868 0 0.9057 0.6842 11 0.992 2 0.9995 0.999 0 0.9952 0.9874 0.9751 0.9677 0.9531 0.944 0 0.3987 注:右上角为bsor值,左下角为Btotal值。 表 14 沿海拔梯度基于有无二元法β多样性的空间轮转组分和嵌套组分
Table 14 There are spatial rotation components and nested components based on β diversity with or without binary method along elevation gradients
区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.3662 0.4615 0.4677 0.520 0 0.5652 0.5098 0.5152 0.7778 0.8125 0.8333 2 0.017 4 0.3462 0.4032 0.4366 0.5217 0.4314 0.4242 0.6667 0.7813 0.8333 3 0.097 5 0.101 0 0.3654 0.3077 0.4038 0.5294 0.5455 0.7037 0.7813 0.8333 4 0.050 5 0.0404 0.0557 0.2581 0.4516 0.5098 0.4848 0.7407 0.8125 0.8333 5 0.027 2 0.0473 0.1629 0.1118 0.3333 0.4118 0.3636 0.5556 0.6563 0.8333 6 0.018 1 0.0068 0.0838 0.0293 0.0654 0.3529 0.303 0 0.4815 0.5938 0.6667 7 0.093 4 0.0932 0.0046 0.0477 0.1438 0.0971 0.1515 0.4815 0.5938 0.500 0 8 0.188 6 0.2104 0.1016 0.1573 0.2774 0.246 0 0.1818 0.4444 0.5938 0.3333 9 0.104 6 0.1497 0.0938 0.102 0 0.2282 0.2269 0.1595 0.0556 0.4444 0.3333 10 0.075 4 0.0828 0.0521 0.0598 0.1541 0.1488 0.093 0 0.0063 0.0471 0 11 0.142 0 0.1407 0.1322 0.1373 0.1444 0.280 0 0.3947 0.4615 0.4242 0.6842 注:右上角为基于有无二元法的空间轮转组分,左下角为嵌套组分。 表 15 沿海拔梯度基于多度β多样性的空间周转组分和树种多度差异组分
Table 15 Spatial turnover components based on multiplicity β diversity and species diversity differences along altitude gradients
区位号 1 2 3 4 5 6 7 8 9 10 11 1 0.3082 0.1537 0.1485 0.4871 0.3613 0.2168 0.1432 0.0656 0.789 0.4387 2 0.0805 0.0824 0.0919 0.2569 0.3002 0.1772 0.1608 0.080 0 0.8705 0.5044 3 0.460 0 0.3941 0.1842 0.1908 0.364 0 0.3233 0.3109 0.1738 0.6986 0.8736 4 0.4714 0.4063 0.0146 0.1528 0.3682 0.2784 0.3113 0.1737 0.6833 0.8841 5 0.2453 0.1681 0.242 0 0.2557 0.1084 0.1392 0.1557 0.087 0.9275 0.6308 6 0.4139 0.3449 0.0569 0.0715 0.1876 0.1743 0.147 0 0.0622 0.7119 0.7939 7 0.5703 0.5133 0.1495 0.1352 0.3778 0.2047 0.1003 0.0623 0.4861 0.9432 8 0.7978 0.7665 0.5337 0.5232 0.687 0 0.5732 0.4175 0.1213 0.156 0 0.5156 9 0.9099 0.895 0 0.7738 0.7679 0.8556 0.7957 0.7059 0.409 0 0.0375 0.226 0 10 0.1987 0.1201 0.2876 0.3009 0.049 0 0.2345 0.4191 0.712 0 0.8682 0 11 0.5535 0.4951 0.1255 0.1111 0.3566 0.1811 0.0245 0.4375 0.718 0 0.3987 注:右上角为树种周转组分,左下角为树种多度差异组分。 -
[1] 叶秀萍,李翠琴,杨伟丽,等. 不同海拔梯度古树物种多样性及其生长特征[J]. 福建林业科技,2021,48(3):79 − 83,92. [2] 刘益曦,胡春,朱圣潮,等. 基于GIS的温州古树资源空间分布特征分析[J]. 风景园林植物,2019,35(5):107 − 111. [3] 谢丽宏,黄钰辉,温小莹,等. 广东省新丰江水库古树资源特征与分布格局[J]. 林业与环境科学,2017,33(4):34 − 38. [4] 尹惠妍,张志伟,侯磊,等. 西藏昌都市居民点散生古树分布特征及主要保护策略分析[J]. 中南林业科技大学学报,2020,40(8):147 − 154. [5] 杜群,陈征海,刘安兴,等. 浙江省古树物种多样性现状研究[J]. 浙江大学学报(农业与生命科学版),2005,31(2):215 − 219. [6] 黄士良,金红霞,冯广平,等. 冀南地区古树名木时空分布及文化价值研究[J]. 河北师范大学学报(自然科学版),2017,41(2):160 − 168. [7] 陈赐赐,杨先友,陈绘画. 仙居县古树的分布区类型用物种多样性[J]. 安徽农业科学,2018,46(34):79 − 82. [8] 吴忠东,杨先友,陈赐赐,等. 仙居县古树资源的空间分布格局[J]. 现代农业科技,2020,(11):160 − 161,163. [9] 吴焕忠,蔡蠕. 古树价值计量评价的研究[J]. 林业建设,2010(1):31 − 35. [10] 王坚娅,丁巧林,李卓,等. 台州市古树名木资源特征和空间分布格局研究[J]. 浙江林业科技,2022,42(4):68 − 74. doi: 10.3969/j.issn.1001-3776.2022.04.011 [11] 黄建辉,高贤明,马克平,等. 地带性森林群落物种多样性的比较研究[J]. 生态学报,1997,17(6):611 − 618. [12] 王冬米,邱智敏,陈征海,等. 台州市乡土木本植物资源调查与特征分析[J]. 浙江林业科技,2017,37(6):51 − 56. [13] 洪小玲,陈蜀蓉,邱智敏,等. 台州市古树名木资源调查和特征分析[J]. 福建林业科技,2022,49(4):102 − 106,132. [14] 李林,魏识广,练琚愉,等. 亚热带不同纬度植物群落物种多样性分布规律[J]. 生态学报,2020,40(4):1249 − 1257. [15] 高贤明,马克平,黄建辉,等. 北京东灵山地区植物群落多样性的研究 Ⅺ. 山地草甸β多样性[J]. 生态学报,1998,18(1):24 − 32. [16] WOLDA H. Similarity indices,sample size and diversity[J]. Oecologia,1981,50: 296 − 302.
[17] 斯幸峰,赵郁豪,陈传武,等. Beta多样性分解:方法、应用与展望[J]. 生物多样性,2017,25(5):464 − 480. doi: 10.17520/biods.2017024 [18] 佘丹琦,张喜亭,肖路,等. 小兴安岭凉水国家级自然保护区植物beta多样性及其影响因素[J]. 生物多样性,2022,30(3):1 − 12. [19] 戴秉国. 长江中下游江湖连通复合体鱼类Beta多样性研究[D]. 合肥:安徽大学,2020. [20] 张金屯. 数量生态学:第三版[M]. 北京:科学出版社,2020:120 − 121. [21] LEGENDRE P,BORCARD D,PERES-NETO P R. Analyzing beta diversity:partitioning the spatial variation of community composition data[J]. Ecological Monographs,2005,75(4):435 − 450. doi: 10.1890/05-0549
[22] LEGENDRE P,CONDIT R. Spatial and temporal analysis of beta diversity in the Barro Colorado Island forest dynamics plot,Panama[J]. Forest Ecosystems,2019,6(1):7 − 17. doi: 10.1186/s40663-019-0164-4
[23] GERING J C,CRIST T O. The alpha-beta-regional relationship:providing new insights into local-regional patterns of species richness and scale dependence of diversity components[J]. Ecology Letters,2002,5(3):433 − 444. doi: 10.1046/j.1461-0248.2002.00335.x
[24] TUOMISTO H. A diversity of beta diversities:straightening up a concept gone awry. Part 1. Defining beta diversity as a function of alpha and gamma diversity[J]. Ecography,2010,33(1):2 − 22. doi: 10.1111/j.1600-0587.2009.05880.x
[25] 张永,施慧,刘璐婷,等. 江苏沿江湖泊湿地越冬水鸟多样性及其影响因素[J]. 湖泊科学,2022,34(6):2005 − 2015. doi: 10.18307/2022.0616 [26] 洪小玲,邱智敏,王松. 台州市乡土树种资源现状调查分析及保护利用对策[J]. 现代农业科技,2023,(7):128 − 133.



 下载:
下载: